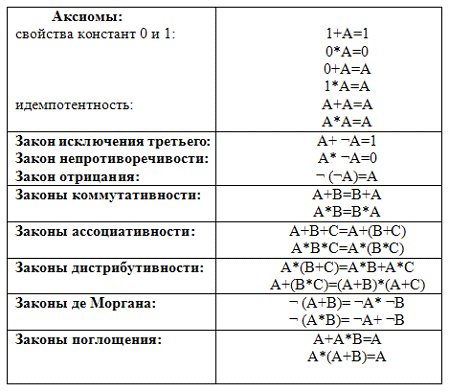
Булева алгебра — основные законы и функции продолжение и окончание с доказательством функций на практике (Часть 2)

Булева алгебра — это важная область математики, которая базируется на принципах двоичной системы исчисления. В предыдущей статье мы рассмотрели основные понятия булевой алгебры и её базовые законы. В этой части мы погрузимся глубже и изучим более сложные функции, которые могут быть использованы для решения различных задач.

Одной из основных функций в булевой алгебре является логическое умножение, или конъюнкция. При конъюнкции двух высказываний, результат будет истинным только тогда, когда оба высказывания истинны. Например, если у нас есть высказывание «Солнце встает на востоке» и высказывание «Солнце заходит на западе», то результат их конъюнкции будет истинным только в случае, если оба высказывания верны.

Другой важной функцией в булевой алгебре является логическое сложение, или дизъюнкция. При дизъюнкции двух высказываний, результат будет истинным, если хотя бы одно из высказываний истинно. Например, если у нас есть высказывание «Сегодня понедельник» и высказывание «Сегодня выходной», то результат их дизъюнкции будет истинным, если хотя бы одно из высказываний верно.

Также существует отрицание, или инверсия. Отрицание высказывания меняет его значение на противоположное. Если изначальное высказывание истинно, то после отрицания оно будет ложным, и наоборот. Например, если у нас есть высказывание «Сегодня солнечный день», его отрицание будет звучать как «Сегодня не солнечный день».

Булева алгебра: основные законы и функции (Часть 2)

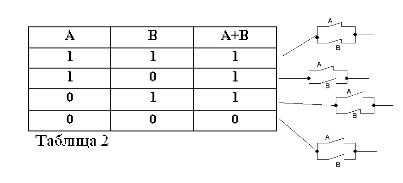
В первой части статьи мы рассмотрели основные понятия булевой алгебры и ее законы. Теперь давайте поговорим о некоторых основных функциях, которые используются в булевой алгебре.

1. Логическая функция NOT (отрицание) — данная функция принимает на вход один аргумент и возвращает его противоположное значение. Если аргумент равен истине (True), то функция вернет ложь (False), и наоборот.

2. Логическая функция AND (конъюнкция) — данная функция принимает на вход два аргумента и возвращает истину (True), если оба аргумента равны истине. В противном случае функция вернет ложь (False).

3. Логическая функция OR (дизъюнкция) — данная функция принимает на вход два аргумента и возвращает истину (True), если хотя бы один из аргументов равен истине. Если оба аргумента равны лжи, функция вернет ложь (False).

4. Логическая функция XOR (исключающее ИЛИ) — данная функция принимает на вход два аргумента и возвращает истину (True), если ровно один из аргументов равен истине. Если оба аргумента равны лжи или оба равны истине, функция вернет ложь (False).

5. Логическая функция NAND (отрицание конъюнкции) — данная функция принимает на вход два аргумента и возвращает ложь (False), если оба аргумента равны истине. Если хотя бы один из аргументов равен лжи, функция вернет истину (True).

6. Логическая функция NOR (отрицание дизъюнкции) — данная функция принимает на вход два аргумента и возвращает ложь (False), если хотя бы один из аргументов равен истине. Если оба аргумента равны лжи, функция вернет истину (True).

Эти основные логические функции являются основой для создания различных комбинаций и составных функций булевой алгебры. Они позволяют производить операции с логическими значениями и решать множество задач, связанных с электроприборами и другими областями, где применяется булева алгебра.

Основы булевой алгебры

Булева алгебра играет важную роль в компьютерной науке и информационных технологиях. Она используется для моделирования и анализа логических операций, комбинационных и последовательных схем, а также для построения логических выражений и изучения их свойств.

Основные операции булевой алгебры — это конъюнкция (логическое И), дизъюнкция (логическое ИЛИ) и отрицание (логическое НЕ). Конъюнкция двух булевых переменных равна истина только в том случае, когда оба операнда истинны. Дизъюнкция двух булевых переменных равна истина, если хотя бы один из операндов истинен. Отрицание булевой переменной меняет ее значение на противоположное.

С помощью операций конъюнкции, дизъюнкции и отрицания можно составлять булевы функции, которые принимают булевы переменные в качестве аргументов и возвращают булево значение. Булевы функции широко применяются в логическом программировании, цифровой логике, криптографии, а также в алгоритмах и структурах данных.

• Операция конъюнкции обозначается символом «∧» или «*», например: A ∧ B.
• Операция дизъюнкции обозначается символом «∨» или «+», например: A ∨ B.
• Операция отрицания обозначается символом «¬» или «-«, например: ¬A.

Вместе с основными операциями булевой алгебры существуют законы, которые описывают алгебраические свойства этих операций. Знание этих законов позволяет упростить логические выражения и улучшить эффективность выполнения логических операций.

Определение и история

До работы Буля логика была рассматривалась в основном как философская дисциплина, но Буль предложил математический подход к логике, основываясь на идеи пропозиций и их связей. Его работа стала отправной точкой для развития булевой алгебры, которая сегодня является неотъемлемой частью информатики и компьютерных наук.

Булева алгебра широко применяется в программировании, цифровой логике, базах данных и других областях, где требуется работа с логическими операциями и истинностными значениями. Ее основные операции – конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ), а также функции, построенные на их основе, позволяют проводить сложные вычисления и принимать решения на основе логических условий.

Операция	Символ	Описание
Конъюнкция (И)	&&	Возвращает истинное значение, если и оба операнда истинны. Иначе возвращает ложное значение.
Дизъюнкция (ИЛИ)	||	Возвращает истинное значение, если хотя бы один из операндов истинен. Иначе возвращает ложное значение.
Отрицание (НЕ)	!	Инвертирует значение операнда: если операнд истинный, то возвращает ложное значение, и наоборот.

Логические операторы

Логические операторы представляют собой специальные символы или ключевые слова, которые используются для комбинирования или изменения логических значений. Они позволяют нам создавать сложные выражения, основанные на истинности или ложности исходных значений.

В языке программирования Булевой алгебры наиболее распространенные логические операторы — это «И» (AND), «ИЛИ» (OR) и «НЕ» (NOT).

Оператор «И» (AND) возвращает истинное значение только если оба операнда истинны. Если хотя бы один из операндов ложен, то результат будет ложным.

Оператор «ИЛИ» (OR) возвращает истинное значение, если хотя бы один из операндов истинен. Если оба операнда ложны, то результат будет ложным.

Оператор «НЕ» (NOT) просто инвертирует логическое значение операнда. Если операнд истинен, то результат будет ложным, и наоборот.

Логические операторы являются основой для создания более сложных логических выражений и для принятия решений в программировании. Они позволяют нам проверять условия и выбирать различные действия, в зависимости от результатов этих проверок.

Булевые функции

Существует несколько основных булевых функций, которые являются основой для построения более сложных логических выражений:

• AND (И) — возвращает истинное значение только тогда, когда все входные аргументы истинны.
• OR (ИЛИ) — возвращает истинное значение, если хотя бы один из входных аргументов истинен.
• NOT (НЕ) — инвертирует значение своего единственного входного аргумента, возвращая истину, если аргумент ложен, и наоборот.
• XOR (Исключающее ИЛИ) — возвращает истину только в том случае, когда количество истинных аргументов нечетное.

Булевые функции используются во многих областях, включая математику, информатику, электронику и программирование. Они позволяют конструировать сложные логические выражения, а также анализировать и управлять логическими состояниями и событиями.

Например, в программировании булевые функции часто используются для принятия решений на основе логических условий. Выражения типа «если это истинно, то сделать это, иначе сделать то» основаны на использовании булевых функций.

Понимание основных булевых функций и их свойств позволяет более эффективно работать с логическими данными и создавать более сложные булевы выражения для решения различных задач.

Представление функций

В таблице истинности каждой функции соответствуют все возможные наборы входных значений и соответствующие им выходные значения. Входные значения представлены различными комбинациями булевых переменных, а выходные значения — результатами работы функции.

Булевый полином представляет функцию в виде алгебраического полинома, состоящего из слагаемых, где каждое слагаемое соответствует одному набору входных значений, для которых функция принимает значение истины. Булевый полином может быть представлен в виде суммы произведений переменных и их отрицаний.

Оба представления функций имеют свои преимущества и недостатки, и выбор способа зависит от конкретной задачи и предпочтений разработчика. Знание основных форм представления функций важно для работы с булевой алгеброй и решения задач логического проектирования.

Основные булевы функции

1. Функция НЕ (NOT)

Функция НЕ принимает один аргумент и возвращает значение, противоположное данному аргументу. Если аргумент истинный (true), функция НЕ вернет ложное значение (false), и наоборот. Функция НЕ обозначается символом «¬».

2. Функция И (AND)

Функция И принимает два аргумента и возвращает истинное значение (true) только в том случае, если оба аргумента истинны. Если хотя бы один из аргументов ложен, функция И вернет ложное значение (false). Функция И обозначается символом «∧».

3. Функция ИЛИ (OR)

Функция ИЛИ принимает два аргумента и возвращает истинное значение (true), если хотя бы один из аргументов истинен. Если оба аргумента ложны, функция ИЛИ вернет ложное значение (false). Функция ИЛИ обозначается символом «∨».

Эти основные булевы функции являются базовыми строительными блоками для решения различных логических задач и формирования более сложных булевых выражений.

Дополнительные булевы функции

Вместе с основными булевыми функциями (И, ИЛИ, НЕ), существует также ряд дополнительных булевых функций, которые могут быть полезны при решении разнообразных задач.

• Исключающее ИЛИ (XOR) — возвращает истину только если один из операндов истинный, но не оба одновременно.
• Импликация — возвращает ложь только если первый операнд истинен, а второй операнд ложен.
• Эквивалентность — возвращает истину только если оба операнда имеют одно и то же значение.
• Штрих Шеффера — является отрицанием операции И (ИЛИ) и возвращает истину, только если оба операнда ложны.
• Стрелка Пирса — является отрицанием операции ИЛИ (И) и возвращает истину, только если оба операнда ложны.

Эти функции могут быть представлены в виде таблицы истинности, где значения операндов и результата отображаются в виде 0 (ложь) или 1 (истина).

Законы булевой алгебры

Булева алгебра представляет собой математическую систему, основанную на принципах двоичной логики. Она используется для описания и анализа логических выражений, которые состоят из булевых переменных (true/false) и операторов (AND, OR, NOT).

В булевой алгебре существуют несколько основных законов, которые позволяют упростить логические выражения и проводить логические операции более эффективно. Некоторые из этих законов включают в себя коммутативность, ассоциативность, дистрибутивность и дополнительность.

Закон коммутативности гласит, что порядок операндов в логическом выражении не влияет на результат. Например, выражение A AND B эквивалентно выражению B AND A.

Закон ассоциативности утверждает, что группировка операндов не влияет на результат. Например, выражение (A AND B) AND C эквивалентно выражению A AND (B AND C).

Дистрибутивный закон гласит, что операции AND и OR можно распределить друг относительно друга. Например, выражение A AND (B OR C) эквивалентно выражению (A AND B) OR (A AND C).

Закон дополнительности утверждает, что дополнение выражения (NOT A) равно выражению A. Например, NOT (NOT A) эквивалентно выражению A.

Эти законы булевой алгебры являются основой для упрощения логических выражений и облегчают процесс работы с булевыми функциями и операторами.

Закон	Формулировка	Пример
Коммутативность	A AND B = B AND A	0 AND 1 = 1 AND 0 = 0
Ассоциативность	(A AND B) AND C = A AND (B AND C)	(0 AND 1) AND 1 = 0 AND (1 AND 1) = 0
Дистрибутивность	A AND (B OR C) = (A AND B) OR (A AND C)	0 AND (1 OR 1) = (0 AND 1) OR (0 AND 1) = 0
Дополнительность	NOT (NOT A) = A	NOT (NOT 0) = 0

Использование этих законов помогает упростить логические выражения и проводить логические операции более эффективно в булевой алгебре. Знание этих законов позволяет анализировать и решать сложные логические задачи.

Основные законы

Булева алгебра основана на нескольких основных законах. Знание этих законов помогает в работе с булевыми значениями и функциями и позволяет упрощать и анализировать логические выражения.

Закон идемпотентности: Если применить операцию И (AND) или ИЛИ (OR) к одной и той же переменной дважды, то она останется неизменной.

Закон коммутативности: Порядок операндов в операциях И (AND) или ИЛИ (OR) не влияет на результат выражения.

Закон ассоциативности: При операциях И (AND) или ИЛИ (OR) ассоциативность определяет, какие операции следует выполнить первыми.

Закон дистрибутивности: Дистрибутивность позволяет связывать операции И (AND) или ИЛИ (OR) через другие операции.

Закон поглощения: Если операция И (AND) или ИЛИ (OR) применяется к переменной и самой себе, результатом всегда будет соответствующее значение этой переменной.

Закон де Моргана: Позволяет заменить отрицание совокупности операций И (AND) или ИЛИ (OR) отрицанием отдельных операндов.

Закон двойного отрицания: Если применить двойное отрицание к любому выражению, результат будет эквивалентен исходному выражению.

Знание основных законов булевой алгебры позволяет более легко и эффективно работать с логическими выражениями, упрощать их и строить более сложные логические функции.

Пример применения законов

Давайте рассмотрим пример применения основных законов булевой алгебры на практике. Представим, что у нас есть две переменные, A и B, которые могут принимать значения «истина» (1) или «ложь» (0). Используя основные функции и законы булевой алгебры, мы можем легко решить различные задачи.

Предположим, у нас есть следующие значения переменных:

A	B
1	0

Сначала, применим закон де Моргана для отрицания конъюнкции (ИЛИ). Согласно закону де Моргана, отрицание конъюнкции A AND B эквивалентно дизъюнкции (ИЛИ) отрицаний A и B. Если мы применим этот закон, получим:

NOT (A AND B) = NOT A OR NOT B

NOT (1 AND 0) = NOT 1 OR NOT 0

1 OR 1 = 0 OR 1

1 = 1

Таким образом, закон де Моргана подтверждается.

Далее, применим закон поглощения. Согласно закону поглощения, конъюнкция A AND (A OR B) эквивалентна самой переменной A. Если мы применим этот закон, получим:

A AND (A OR B) = A

1 AND (1 OR 0) = 1

1 AND 1 = 1

1 = 1

Таким образом, закон поглощения подтверждается.

Это лишь пример использования основных законов булевой алгебры. С их помощью можно решать более сложные задачи, составлять логические выражения и доказывать их эквивалентность, что делает булеву алгебру мощным инструментом логического анализа.

Применение булевой алгебры в электронике

Основной задачей булевой алгебры в электронике является моделирование и проектирование логических функций и схем. Логические функции представляют собой алгоритмы, которые могут принимать значения «истина» (1) или «ложь» (0) и взаимодействовать между собой в соответствии с заданной логикой.

Булева алгебра предоставляет различные операции, такие как «И» (AND), «ИЛИ» (OR), «НЕ» (NOT) и другие, которые позволяют комбинировать логические функции и строить разнообразные логические схемы. Например, с помощью И-ИЛИ схем можно реализовать простые логические элементы, такие как вентили и триггеры.

Применение булевой алгебры в электронике не ограничивается только моделированием и проектированием логических схем. Она также используется при разработке цифровых сигнальных процессоров, микросхем, компьютерных алгоритмов и других электронных устройств. Без булевой алгебры было бы крайне сложно проектировать и анализировать сложные системы, работающие на основе логических принципов.

Логические элементы и схемы

В логической схеме используются различные символы для представления различных логических операций. Например, символ «И» (AND) обозначает логическую операцию конъюнкции, символ «ИЛИ» (OR) обозначает логическую операцию дизъюнкции, символ «НЕ» (NOT) обозначает логическую операцию отрицания.

Логические элементы могут быть объединены в логические схемы для создания более сложных логических операций. Примером такой схемы является схема, представляющая логическое выражение (A ИЛИ B) И НЕ C. Для построения такой схемы используются различные логические элементы, связанные между собой.

Чтобы логическая схема корректно работала, необходимо определить входные сигналы (логические переменные) и правила работы каждого элемента. Входной сигнал может быть равен либо true (логическая единица), либо false (логический ноль), в зависимости от того, выполняется ли условие, которое он представляет. Выходной сигнал зависит от входных сигналов и конфигурации элемента.

Логические элементы и схемы являются основой для построения цифровых схем, которые используются в различных электронных устройствах, таких как компьютеры и микроконтроллеры. Понимание принципов работы логических элементов и схем позволяет разрабатывать и анализировать сложные электронные системы.

Символ	Описание
AND	Логическая операция конъюнкции (логическое «И»)
OR	Логическая операция дизъюнкции (логическое «ИЛИ»)
NOT	Логическая операция отрицания (логическое «НЕ»)

Проектирование цифровых устройств

Цифровые устройства используют булеву алгебру для логического анализа и управления различными сигналами. Они состоят из комбинаций логических элементов, таких как вентили И, ИЛИ и НЕ, которые выполняют различные логические операции над битами информации.

Проектирование цифровых устройств начинается с создания схемы, которая описывает взаимосвязь и взаимодействие логических элементов. На этом этапе применяются основные законы и функции булевой алгебры.

Далее следует этап моделирования и проверки работы схемы с помощью специального программного обеспечения или физического прототипирования. Во время моделирования можно проверить корректность работы схемы и определить ее эффективность в решении задачи.

После успешного моделирования осуществляется фаза создания физического устройства на основе схемы. Используется специальное программное обеспечение и технологии производства для создания и монтажа компонентов устройства.

Наконец, производится тестирование готового устройства для проверки его работоспособности и соответствия спецификациям. В случае необходимости можно вносить коррективы и оптимизировать устройство для улучшения его производительности.

Булева алгебра и проектирование цифровых устройств тесно связаны, и умение применять основные законы и функции, а также понимать принципы проектирования, является важным навыком для специалистов в области электроники и компьютерных наук.

Примеры электроприборов

Булева алгебра находит широкое применение в различных электроприборах, повседневно используемых людьми:

— Световые выключатели: они имеют два состояния, включено (1) или выключено (0), и могут быть объединены с помощью логических операций для управления группами световых приборов;

— Дверные замки: они также имеют два состояния, открыто (1) или закрыто (0), и могут быть программированы с помощью логических функций для контроля доступа;

— Кнопки на электронных устройствах: нажатие на кнопку приводит к изменению сигнала с 0 на 1 или наоборот, что позволяет управлять функциональностью устройства;

— Автоматические датчики движения: они позволяют обнаруживать наличие движения в помещении и использовать эту информацию для включения и выключения света или других устройств.

Видео: