Системы счисления чисел: от бинарной до шестнадцатеричной

Система счисления — это способ представления чисел с помощью определенного набора символов или цифр. В разных культурах и математических системах используются различные системы счисления, каждая из которых имеет свои особенности и правила.

Наиболее распространенная система счисления — десятичная, которая основана на порядке чисел от 0 до 9. В этой системе каждая цифра имеет свою весовую степень, определяющую ее значение. Например, число 123 представляет собой сумму 1*10^2 + 2*10^1 + 3*10^0.

Однако помимо десятичной системы существует множество других систем счисления, в которых основание может быть любым. Например, в двоичной системе счисления основание равно 2, поэтому она использует только две цифры — 0 и 1. В восьмеричной системе основание равно 8, поэтому она использует восемь цифр — от 0 до 7.

Каждая система счисления имеет свои преимущества и недостатки. Например, двоичная система широко используется в компьютерных науках из-за своей простоты и относительной легкости в реализации. Однако для представления больших чисел она требует большого количества цифр, что может затруднить чтение и понимание таких чисел.

Содержание

Десятичная система счисления

Десятичная система счисления является одной из наиболее распространенных и удобных систем счисления, которая основана на числе 10. В этой системе используются 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждая цифра в десятичной системе счисления имеет свое собственное значение, которое зависит от ее позиции в числе.

Например, число 437 в десятичной системе разбивается на три цифры: 4, 3 и 7. Число 4 имеет значение 400, число 3 имеет значение 30, а число 7 имеет значение 7. Эти значения складываются, чтобы получить итоговое значение числа 437.

Десятичная система счисления часто используется в повседневной жизни, например, при подсчете денег, измерении времени и т.д. В программировании и компьютерных науках также широко применяется десятичная система для представления чисел и выполнения различных математических операций.

Для удобства работы с большими числами десятичная система счисления использует позиционную нотацию, в которой каждой цифре присваивается позиция в числе, определяющая ее вес или значение. Например, в числе 437 позиция цифры 4 равна 100, позиция цифры 3 равна 10, а позиция цифры 7 равна 1.

Основная информация

Система счисления чисел – это способ представления чисел с помощью цифр и их расположения в разрядах

Наиболее распространенной системой счисления является десятичная система, основанная на числе 10. В этой системе используются цифры от 0 до 9, и любое число представляется комбинацией этих цифр.

Однако существуют и другие системы счисления, такие как двоичная, восьмеричная и шестнадцатеричная. В двоичной системе используются только две цифры – 0 и 1. В восьмеричной системе используются восемь цифр – от 0 до 7. А в шестнадцатеричной системе используются шестнадцать цифр – от 0 до 9 и от A до F.

Кроме того, существуют и нестандартные системы счисления, например, система счисления с основанием 60, которую используют некоторые народы для измерения времени.

Каждая система счисления имеет свои особенности и применяется в разных областях. Например, двоичная система широко применяется в электронике и компьютерах, где единицей является наличие или отсутствие электрического сигнала.

Преимущества и недостатки

Преимущества систем счисления

Универсальность: системы счисления позволяют представлять числа любого размера и значения.
Интуитивность: в большинстве систем счисления, числа записываются последовательностью цифр, что делает их понятными и удобными для работы.
Гибкость: системы счисления могут быть основаны на различных числах и символах, что дает возможность использовать разные системы в разных областях науки и техники.
Удобство в вычислениях: в разных системах счисления можно легко выполнять основные арифметические операции — сложение, вычитание, умножение и деление.

Недостатки систем счисления

Перегрузка информацией: в некоторых системах счисления, особенно с большим основанием, числа могут занимать большой объем памяти или быть трудными для восприятия.
Ограниченность точности: в системах с ограниченной точностью, представление некоторых чисел может быть приближенным и потерять некоторую точность при вычислениях.
Сложность перевода: перевод чисел из одной системы счисления в другую может быть сложным и требовать дополнительных вычислений.

Двоичная система счисления

Двоичная система счисления является одной из самых распространенных систем счисления после десятичной. Она основана на принципе использования только двух цифр — 0 и 1. Этот принцип является основой для работы с компьютерами и цифровыми устройствами.

В двоичной системе счисления каждая цифра имеет вес, который увеличивается в два раза с каждым следующим разрядом. Например, в двоичной системе число 1010 будет означать (1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (0 * 2^0) = 8 + 0 + 2 + 0 = 10.

Двоичная система счисления широко используется в компьютерных науках и информатике. Компьютеры хранят данные и выполняют вычисления в двоичном формате, так как это естественно для работы с двумя состояниями — вкл/выкл.

Двоичная система счисления также позволяет представлять данные в виде битов и байтов, где бит — это одна цифра двоичной системы, а байт — это группа из 8 битов. Комбинация байтов позволяет представлять большие числа и хранить информацию, такую как текст, изображения и звук.

Преобразование чисел из десятичной системы в двоичную и наоборот является важным навыком для программистов и специалистов в области компьютерной науки. Оно позволяет понимать, как компьютеры хранят и обрабатывают информацию, и позволяет эффективно работать с двоичными данными.

Основная информация

Система счисления чисел — это способ представления чисел при помощи цифр и разрядов. Все цифры в системе счисления имеют определенный вес, который зависит от их позиции в числе.

В настоящее время наиболее распространенная система счисления — десятичная система счисления. В ней используются 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Любое число в десятичной системе счисления может быть представлено с помощью этих цифр.

Однако помимо десятичной системы счисления существуют и другие системы: двоичная, восьмеричная, шестнадцатеричная и др. В двоичной системе счисления используются всего две цифры: 0 и 1. В восьмеричной системе счисления используют 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. В шестнадцатеричной системе счисления используют 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Перевод чисел из одной системы счисления в другую осуществляется путем разложения числа на разряды и умножения каждого разряда на соответствующий ему вес. Вес цифр в различных системах счисления меняется. Так, в двоичной системе счисления вес каждого разряда увеличивается вдвое, в восьмеричной — восемь раз, а в шестнадцатеричной — шестнадцать раз.

Использование в компьютерах

Использование систем счисления чисел является неотъемлемой частью работы компьютеров. В компьютерных системах наиболее распространенной системой счисления является двоичная система. Почему именно двоичная? Потому что компьютеры работают на основе двух состояний: включено и выключено, что и прекрасно соответствует принципу двоичной системы счисления.

Двоичная система счисления используется в компьютерах для кодирования информации. Для представления чисел в компьютерах используются двоичные числа, состоящие из нулей и единиц. Каждая позиция в числе имеет свой вес: первая позиция имеет вес 2^0, вторая позиция — 2^1, третья позиция — 2^2 и так далее. Таким образом, компьютеры могут представлять и обрабатывать числа в двоичной системе счисления.

Кроме двоичной системы счисления, в компьютерах также используется десятичная система счисления. Десятичная система счисления используется для представления чисел, которые компьютер получает от пользователя или выводит на экран. Для взаимодействия с людьми компьютеры обычно используют десятичные числа, так как они более привычны и понятны для большинства людей.

В компьютерах также есть возможность использовать другие системы счисления, такие как восьмеричная и шестнадцатеричная. Они используются для представления чисел в компьютерных системах с большими или непростыми значениями. Например, восьмеричная система используется в операционных системах для представления прав доступа к файлам и папкам, а шестнадцатеричная система используется для представления цветовых значений в графическом программном обеспечении.

Шестнадцатеричная система счисления

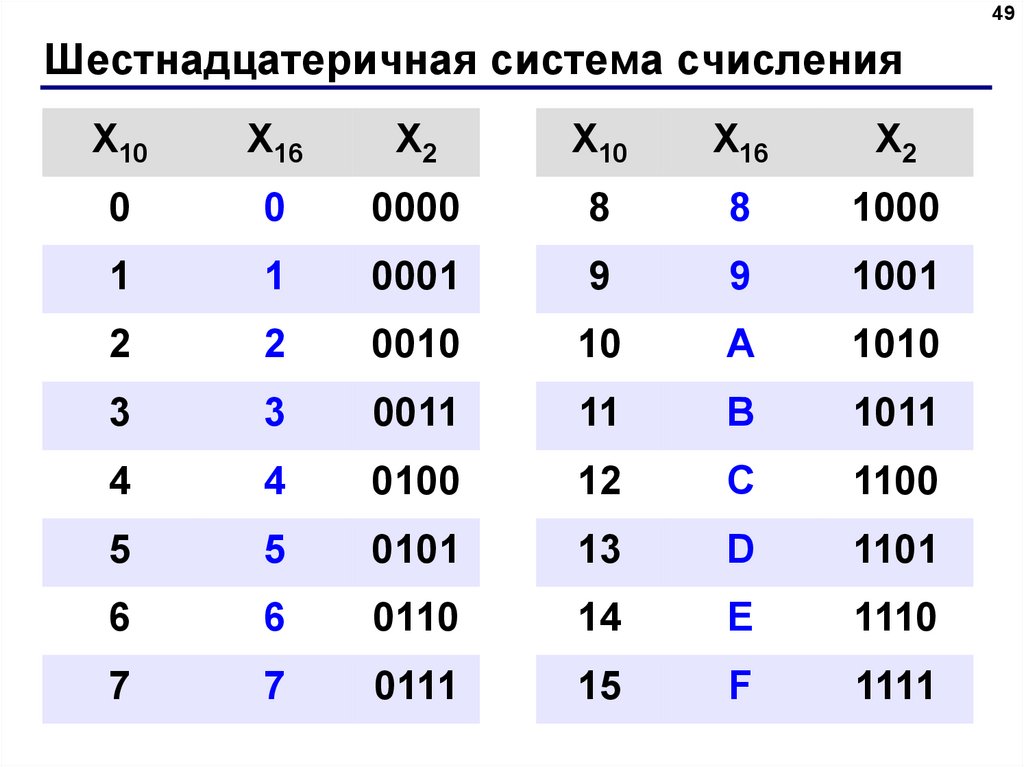
Шестнадцатеричная система счисления — это система счисления, основанная на числе 16. В отличие от десятичной системы, которая использует 10 цифр (от 0 до 9), шестнадцатеричная система использует 16 цифр (от 0 до 9 и от A до F).

В шестнадцатеричной системе счисления каждая цифра представляет определенное число. Цифры от 0 до 9 имеют те же значения, что и в десятичной системе, тогда как буквы от A до F представляют числа от 10 до 15 соответственно.

Шестнадцатеричную систему счисления часто используют в программировании и информационных технологиях. Она удобна для представления больших чисел с меньшим количеством символов, поскольку каждая цифра шестнадцатеричного числа представляет 4 двоичные цифры (биты). Также шестнадцатеричные числа не сложно переводить в двоичную систему или из двоичной системы обратно в шестнадцатеричную.

Для обозначения шестнадцатеричных чисел перед числом иногда ставят префикс «0x». Например, число 10 в шестнадцатеричной системе будет обозначаться как 0xA, а число 15 — как 0xF.

Основная информация

Система счисления — это способ представления чисел с помощью символов. Существует несколько различных систем счисления, которые используются для разных целей.

Наиболее распространенная система счисления — десятичная. Она основана на использовании десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В десятичной системе счисления каждая цифра имеет свое место в числе и влияет на его значение.

Однако, помимо десятичной системы, существуют и другие системы счисления, такие как двоичная, восьмеричная и шестнадцатеричная. В двоичной системе счисления используются только две цифры: 0 и 1. В восьмеричной системе счисления используются восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. А в шестнадцатеричной системе счисления используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Каждая система счисления имеет свои особенности и применяется в различных областях. Например, двоичная система широко используется в компьютерах для представления и обработки информации.